The broadest definition of weight in this sense is that the weight of an object is the gravitational force on it from the nearest large body, such as Earth, the Moon, the Sun, and so on. This is the most common and useful definition of weight in physics. It differs dramatically, however, from the definition of weight used by NASA and the popular media in relation to space travel and exploration. When they speak of “weightlessness” and “microgravity,” they are really referring to the phenomenon we call “freefall” in physics. We shall use the above definition of weight, and we will make careful distinctions between free-fall and actual weightlessness.

It is important to be aware that weight and mass are very different physical quantities, although they are closely related. Mass is the quantity of matter (how much “stuff”) and does not vary in classical physics, whereas weight is the gravitational force and does vary depending on gravity.

It is tempting to equate the two, since most of our examples take place on Earth, where the weight of an object only varies a little with the location of the object. Furthermore, the terms mass and weight are used interchangeably in everyday language; for example, our medical records often show our “weight” in kilograms, but never in the correct units of newtons.

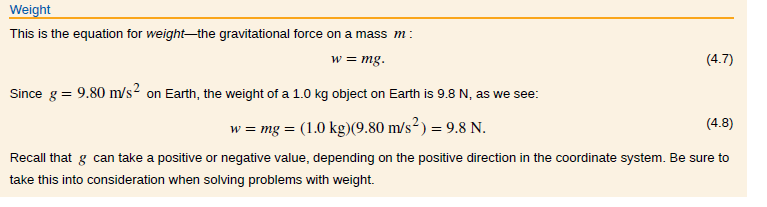
When the net external force on an object is its weight, we say that it is in free-fall. That is, the only force acting on the object is the force of gravity. In the real world, when objects fall downward toward Earth, they are never truly in free-fall because there is always some upward force from the air acting on the object.

The acceleration due to gravity g varies slightly over the surface of Earth, so that the weight of an object depends on location and is not an intrinsic property of the object. Weight varies dramatically if one leaves Earth’s surface. On the Moon, for example, the acceleration due to gravity is only 1.67 m/s^2 . A 1.0-kg mass thus has a weight of 9.8 N on Earth and only about 1.7 N on the Moon.

Use of beam balance to measure mass and weight:

This OpenStax book is available for free at http://cnx.org/content/col11406/1.14