-
PART 1 INTERACTION OF MATTER, SPACE & TIME
-
Concepts of Matter
Simple structure of matter should be discussed. Three physics states of matter, namely solid, liquid and gas should be treated. Evidence of the particle nature of matter e.g. Brownian motion experiment, Kinetic theory of matter. Use of the theory to explain; states of matter (solid, liquid and gas), pressure in a gas, evaporation and boiling; cohesion, adhesion, capillarity. Crystalline and amorphous substances to be compared (Arrangement of atoms in crystalline structure to be described e.g. face centred, body centred.
-
Fundamental and derived quantities and units
Length, mass, time, electric current luminous intensity, thermodynamic temperature, amount of substance as examples of fundamental quantities and m, kg, s, A, cd, K and mol as their respective units. Volume, density and speed as derived quantities and m3, kgm-3 and ms-1 as their respective units.
-
Position, distance and displacement
Position of objects in space using the X,Y,Z axes should be mentioned. Use of string, metre rule, vernier calipers and micrometer screw gauge. Degree of accuracy should be noted. Metre (m) as unit of distance. Use of compass and a protractor. Graphical location and directions by axes to be stressed.
-
Mass and weight
Use of lever balance and chemical/beam balance to measure mass and spring balance to measure weight. Mention should be made of electronic/digital balance. Kilogram (kg) as unit of mass and newton (N) as unit of weight.
-
Time
The use of heart-beat, sand-clock, ticker-timer, pendulum and stopwatch/clock. Second(s) as unit of time.
-
Fluid at rest
Experimental determination for solids and liquids. Concept and definition of pressure. Pascal’s principle, application of principle to hydraulic press and car brakes. Dependence of pressure on the depth of a point below a liquid surface. Atmospheric pressure. Simple barometer, manometer, siphon, syringe and pump. Determination of the relative density of liquids with U-tube and Hare’s apparatus. Identification of the forces acting on a body partially or completely immersed in a fluid. Use of the principle to determine the relative densities of solids and liquids. Establishing the conditions for a body to float in a fluid. Applications in hydrometer, balloons, boats, ships, submarines etc.
-
Motion
Only qualitative treatment is required. Illustration should be given for the various types of motion. Numerical problems on co-linear motion may be set. Force as cause of motion. Push and pull These are field forces namely; electric and magnetic attractions and repulsions; gravitational pull. Frictional force between two stationary bodies (static) and between two bodies in relative motion (dynamic). Coefficients of limiting friction and their determinations. Advantages of friction e.g. in locomotion, friction belt, grindstone. Disadvantages of friction e.g reduction of efficiency, wear and tear of machines. Methods of reducing friction; e.g. use of ball bearings, rollers, streamlining and lubrication. Definition and effects. Simple explanation as extension of friction in fluids. Fluid friction and its application in lubrication should be treated qualitatively. Terminal velocity and its determination. Experiments with a string tied to a stone at one end and whirled around should be carried out to (i) demonstrate motion in a Vertical/horizontal circle. (i) show the difference between angular speed and velocity. (ii) Draw a diagram to illustrate centripetal force. Banking of roads in reducing sideways friction should be qualitatively discussed.
-
Speed and velocity
Metre per second (ms-1) as unit of speed/velocity. Ticker-timer or similar devices should be used to determine speed/velocity. Definition of velocity as ∆ s ∆t. Determination of instantaneous speed/velocity from distance/displacement-time graph and by calculation. Unit of acceleration as ms-2 Ticker timer or similar devices should be used to determine acceleration. Definition of acceleration as ∆ v ∆t . Determination of acceleration and displacement from velocity-time graph Use of equations to solve numerical problems.
-
Scalars and vectors
Mass, distance, speed and time as examples of scalars. Weight, displacement, velocity and acceleration as examples of vectors. Use of force board to determine the resultant of two forces. Obtain the resultant of two velocities analytically and graphically. Torque/Moment of force. Simple treatment of a couple, e.g. turning of water tap, corkscrew and steering wheel.) Use of force board to determine resultant and equilibrant forces. Treatment should include resolution of forces into two perpendicular directions and composition of forces Parallelogram of forces. Triangle of forces. Should ne treated experimentally. Treatment should include stable, unstable and neutral equilibra. Use of a loaded test-tube oscillating vertically in a liquid, simple pendulum, spiral spring and bifilar suspension to demonstrate simple harmonic motion.
-
Simple harmonic motion
Relate linear and angular speeds, linear and angular accelerations. Experimental determination of ‘g’ with the simple pendulum and helical spring. The theory of the principles should be treated but derivation of the formula for ‘g’ is not required Simple problems may be set on simple harmonic motion. Mathematical proof of simple harmonic motion in respect of spiral spring, bifilar suspension and loaded test-tube is not required.
-
Newton’s laws of motion:
Distinction between inertia mass and weight Use of timing devices e.g. ticker-timer to determine the acceleration of a falling body and the relationship when the accelerating force is constant. Linear momentum and its conservation. Collision of elastic bodies in a straight line. Applications: recoil of a gun, jet and rocket propulsions.
Kinetic Theory of matter and states of matter
Like we already stated, there are at least 3 states of matter:
Three States of Matter:
Matter can exist in several phases. The most common states of matter are this 3:
- Gas
- Liquid
- Solid.
We also said that the state of matter depends primarily on the temperature and pressure applied on the matter. Now let us use Kinetic theory to explain this further.
Kinetic Theory: Atomic and Molecular Explanation of Pressure and Temperature
We have developed macroscopic definitions of pressure and temperature. Pressure is the force divided by the area on which the force is exerted, and temperature is measured with a thermometer. We gain a better understanding of pressure and temperature from the kinetic theory of gases, which assumes that atoms and molecules are in continuous random motion.
Figure 13.20 shows an elastic collision of a gas molecule with the wall of a container, so that it exerts a force on the wall (by Newton’s third law). Because a huge number of molecules will collide with the wall in a short time, we observe an average force per unit area. These collisions are the source of pressure in a gas. As the number of molecules increases, the number of collisions and thus the pressure increase. Similarly, the gas pressure is higher if the average velocity of molecules is higher. The actual relationship is derived in the Things Great and Small feature below. The following relationship is found:
What can we learn from this atomic and molecular version of the ideal gas law? We can derive a relationship between temperature and the average translational kinetic energy of molecules in a gas.
Phase Changes
Up to now, we have considered the behavior of ideal gases. Real gases are like ideal gases at high temperatures. At lower temperatures, however, the interactions between the molecules and their volumes cannot be ignored. The molecules are very close (condensation occurs) and there is a dramatic decrease in volume, as seen in Figure 13.26. The substance changes from a gas to a liquid. When a liquid is cooled to even lower temperatures, it becomes a solid. The volume never reaches zero because of the finite volume of the molecules.
High pressure may also cause a gas to change phase to a liquid. Carbon dioxide, for example, is a gas at room temperature and atmospheric pressure, but becomes a liquid under sufficiently high pressure. If the pressure is reduced, the temperature drops and the liquid carbon dioxide solidifies into a snow-like substance at the temperature – 78ºC . Solid CO2 is called “dry ice.”
Another example of a gas that can be in a liquid phase is liquid nitrogen (LN2) . LN2 is made by liquefaction of atmospheric air (through compression and cooling). It boils at 77 K (–196ºC) at atmospheric pressure. LN2 is useful as a refrigerant and allows for the preservation of blood, sperm, and other biological materials. It is also used to reduce noise in electronic sensors and equipment, and to help cool down their current-carrying wires. In dermatology, LN2 is used to freeze and painlessly remove warts and other growths from the skin.
PV Diagrams
We can examine aspects of the behavior of a substance by plotting a graph of pressure versus volume, called a PV diagram. When the substance behaves like an ideal gas, the ideal gas law describes the relationship between its pressure and volume.
That is,
Table 13.3 Critical Temperatures and Pressures
| Substance | Critical temperature | Critical pressure | ||
| K | ºC | Pa | atm | |
| Water | 647.4 | 374.3 | 22.12×10^6 | 219.0 |
| Sulfur dioxide | 430.7 | 157.6 | 7.88×10^6 | 78.0 |
| Ammonia | 405.5 | 132.4 | 11.28×10^6 | 111.7 |
| Carbon dioxide | 304.2 | 31.1 | 7.39×10^6 | 73.2 |
| Oxygen | 154.8 | -118.4 | 5.08×10^6 | 50.3 |
| Nitrogen | 126.2 | -146.9 | 3.39×10^6 | 33.6 |
| Hydrogen | 33.3 | -239.9 | 1.30×10^6 | 12.9 |
| Helium | 5.3 | -267.9 | 0.229×10^6 | 2.27 |
Phase Diagrams
The plots of pressure versus temperatures provide considerable insight into thermal properties of substances. There are well defined regions on these graphs that correspond to various phases of matter, so PT graphs are called phase diagrams.
Figure 13.28 shows the phase diagram for water. Using the graph, if you know the pressure and temperature you can determine the phase of water. The solid lines—boundaries between phases—indicate temperatures and pressures at which the phases coexist (that is, they exist together in ratios, depending on pressure and temperature). For example, the boiling point of water is 100ºC at 1.00 atm. As the pressure increases, the boiling temperature rises steadily to 374ºC at a pressure of 218 atm. A pressure cooker (or even a covered pot) will cook food faster because the water can exist as a liquid at temperatures greater than 100ºC without all boiling away. The curve ends at a point called the critical point, because at higher temperatures the liquid phase does not exist at any pressure. The critical point occurs at the critical temperature, as you can see for water from Table 13.3. The critical temperature for oxygen is – 118ºC , so oxygen cannot be liquefied above this temperature.
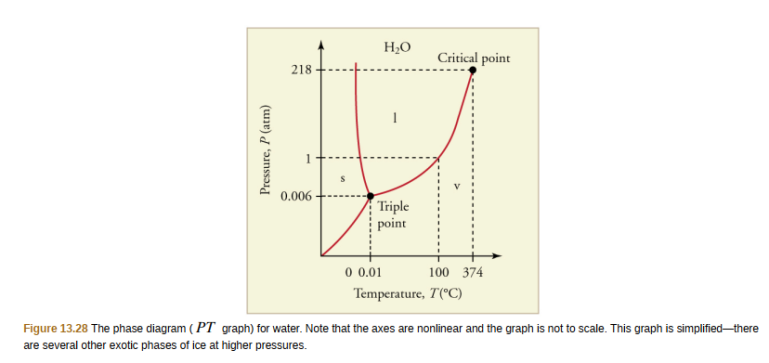
Similarly, the curve between the solid and liquid regions in Figure 13.28 gives the melting temperature at various pressures. For example, the melting point is 0ºC at 1.00 atm, as expected. Note that, at a fixed temperature, you can change the phase from solid (ice) to liquid (water) by increasing the pressure. Ice melts from pressure in the hands of a snowball maker. From the phase diagram, we can also say that the melting temperature of ice falls with increased pressure. When a car is driven over snow, the increased pressure from the tires melts the snowflakes; afterwards the water refreezes and forms an ice layer.
At sufficiently low pressures there is no liquid phase, but the substance can exist as either gas or solid. For water, there is no liquid phase at pressures below 0.00600 atm. The phase change from solid to gas is called sublimation. It accounts for large losses of snow pack that never make it into a river, the routine automatic defrosting of a freezer, and the freeze-drying process applied to many foods. Carbon dioxide, on the other hand, sublimates at standard atmospheric pressure of 1 atm. (The solid form of CO2 is known as dry ice because it does not melt. Instead, it moves directly from the solid to the gas state.)
All three curves on the phase diagram meet at a single point, the triple point, where all three phases exist in equilibrium. For water, the triple point occurs at 273.16 K (0.01ºC) , and is a more accurate calibration temperature than the melting point of water at 1.00 atm, or 273.15 K (0.0ºC) . See Table 13.4 for the triple point values of other substances.
Equilibrium
Liquid and gas phases are in equilibrium at the boiling temperature. (See Figure 13.29.) If a substance is in a closed container at the boiling point, then the liquid is boiling and the gas is condensing at the same rate without net change in their relative amount.
Molecules in the liquid escape as a gas at the same rate at which gas molecules stick to the liquid, or form droplets and become part of the liquid phase. The combination of temperature and pressure has to be “just right”; if the temperature and pressure are increased, equilibrium is maintained by the same increase of boiling and condensation rates.
Table 13.4 Triple Point Temperatures and Pressures
| Substance | Temperature | Pressure | ||
| K | ºC | Pa | atm | |
| Water | 273.16 | 0.01 | 6.10×10^2 | 0.00600 |
| Carbon dioxide | 216.55 | -56.60 | 5.16×10^5 | 5.11 |
| Sulfur dioxide | 197.68 | -75.47 | 1.67×10^3 | 0.0167 |
| Ammonia | 195.40 | -77.75 | 6.06×10^3 | 0.0600 |
| Nitrogen | 63.18 | -210.0 | 1.25×10^4 | 0.124 |
| Oxygen | 54.36 | -218.8 | 1.52×10^2 | 0.00151 |
| Hydrogen | 13.84 | -259.3 | 7.04×10^3 | 0.0697 |
One example of equilibrium between liquid and gas is that of water and steam at 100ºC and 1.00 atm. This temperature is the boiling point at that pressure, so they should exist in equilibrium. Why does an open pot of water at 100ºC boil completely away? The gas surrounding an open pot is not pure water: it is mixed with air. If pure water and steam are in a closed container at 100ºC and 1.00 atm, they would coexist—but with air over the pot, there are fewer water molecules to condense, and water boils. What about water at 20.0ºC and 1.00 atm? This temperature and pressure correspond to the liquid region, yet an open glass of water at this temperature will completely evaporate. Again, the gas around it is air and not pure water vapor, so that the reduced evaporation rate is greater than the condensation rate of water from dry air. If the glass is sealed, then the liquid phase remains. We call the gas phase a vapor when it exists, as it does for water at 20.0ºC , at a temperature below the boiling temperature.
Check Your Understanding
Explain why a cup of water (or soda) with ice cubes stays at 0ºC , even on a hot summer day.
Solution
The ice and liquid water are in thermal equilibrium, so that the temperature stays at the freezing temperature as long as ice remains in the liquid. (Once all of the ice melts, the water temperature will start to rise.)
Vapor Pressure, Partial Pressure, and Dalton’s Law
Vapor pressure is defined as the pressure at which a gas coexists with its solid or liquid phase. Vapor pressure is created by faster molecules that break away from the liquid or solid and enter the gas phase. The vapor pressure of a substance depends on both the substance and its temperature—an increase in temperature increases the vapor pressure.
Partial pressure is defined as the pressure a gas would create if it occupied the total volume available. In a mixture of gases, the total pressure is the sum of partial pressures of the component gases, assuming ideal gas behavior and no chemical reactions between the components. This law is known as Dalton’s law of partial pressures, after the English scientist John Dalton (1766–1844), who proposed it. Dalton’s law is based on kinetic theory, where each gas creates its pressure by molecular collisions, independent of other gases present. It is consistent with the fact that pressures add according to Pascal’s Principle.
Thus water evaporates and ice sublimates when their vapor pressures exceed the partial pressure of water vapor in the surrounding mixture of gases. If their vapor pressures are less than the partial pressure of water vapor in the surrounding gas, liquid droplets or ice crystals (frost) form.
Check Your UnderstandingIs energy transfer involved in a phase change? If so, will energy have to be supplied to change phase from solid to liquid and liquid to gas? What about gas to liquid and liquid to solid? Why do they spray the orange trees with water in Aba, Abia state when the temperatures are near or just below freezing?
Solution
Yes, energy transfer is involved in a phase change. We know that atoms and molecules in solids and liquids are bound to each other because we know that force is required to separate them. So in a phase change from solid to liquid and liquid to gas, a force must be exerted, perhaps by collision, to separate atoms and molecules. Force exerted through a distance is work, and energy is needed to do work to go from solid to liquid and liquid to gas. This is intuitively consistent with the need for energy to melt ice or boil water. The converse is also true. Going from gas to liquid or liquid to solid involves atoms and molecules pushing together, doing work and releasing energy.
This OpenStax book is available for free at http://cnx.org/content/col11406/1.14